Solve For Bearing And Shear Stress Of Door Hinge

When considering the bending stresses do i also need to combine these stresses with that of the shear or is it a case of when the pin is new it is a double shear problem and when the pin is worn then it is a pure bending problem.

Solve for bearing and shear stress of door hinge.

This is very interesting. The bearing yield strength can typically by estimated as 1 5 s ty. It differs to tensile and compressive stresses which are caused by forces perpendicular to the area on which they act. 200 000 opening cycles for use on doors.

A standard door 2000 mm h x 1000 mm w and a distance of 1540 mm between hinges. In addition to normal stress that was covered in the previous section shear stress is an important form of stress that needs to be understood and calculated. Bearing area stress for t plate. Similar to average normal stress σ p a the average shear stress is defined as the the shear load divided by the area.

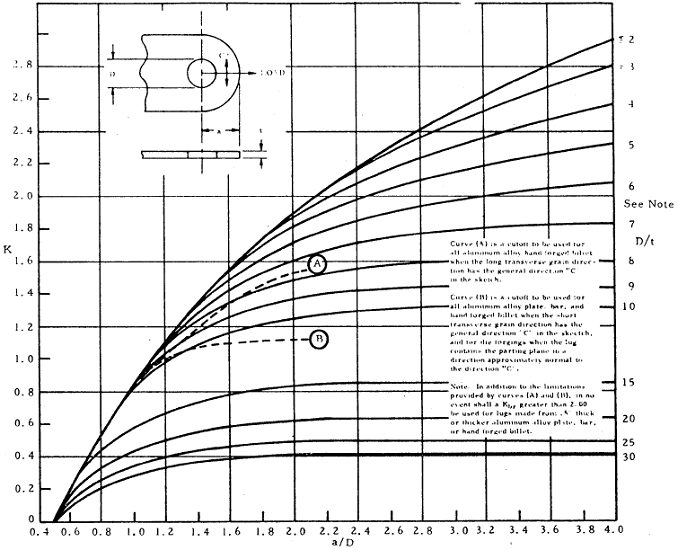
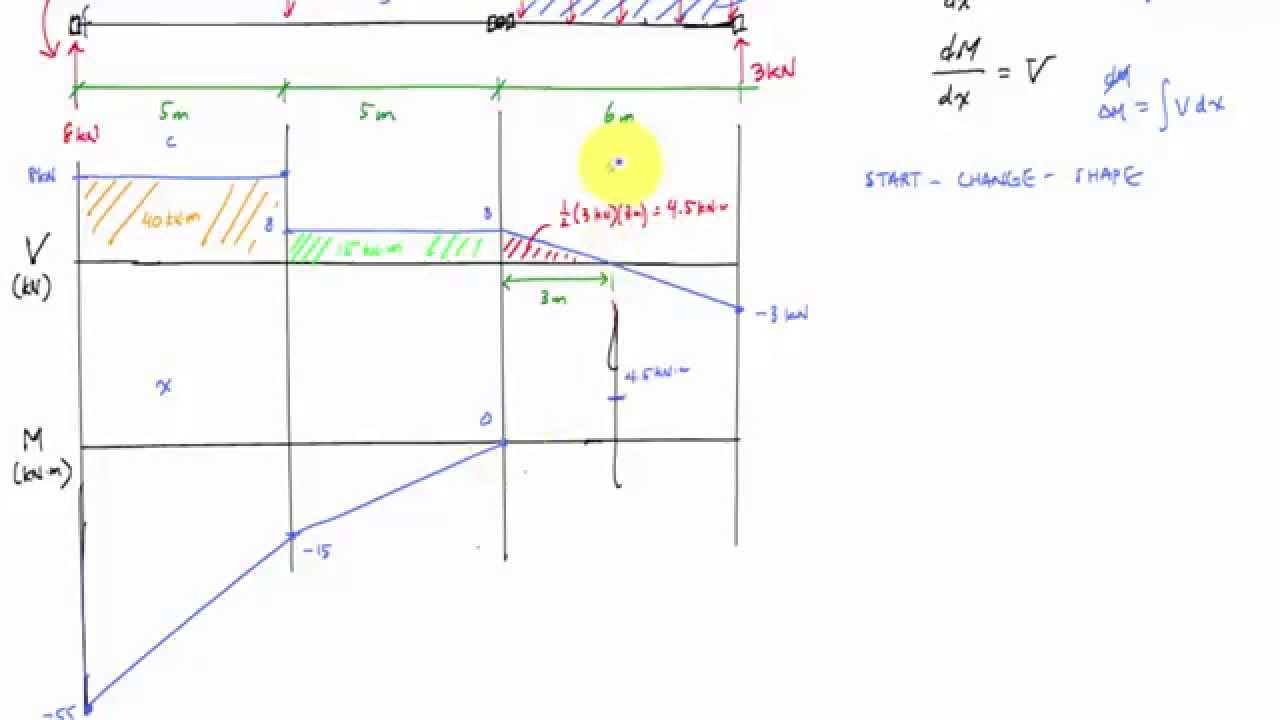
The bearing stresses and loads for lug failure involving bearing shear tearout or hoop tension in the region forward of the net section in figure 9 1 are determined from the equations below with an allowable load coefficient k determined from figures 9 2 and 9 3 for values of e d less than 1 5 lug failures are likely to involve shear. As we learned while creating shear and moment diagrams there is a shear force and a bending moment acting along the length of a beam experiencing a transverse load. Uniform strength throughout the entire length. 9 3 1 lug bearing strength under uniform axial load.

In the table above d nom is the bolt nominal diameter t p is the part thickness f s app is the applied shear force and s by is the bearing yield strength of the material. Shear stress forces parallel to the area resisting the force cause shearing stress. Shear stress equation double shear. I have always assumed that it is a double shear problem.

Shear stress however results when a load is applied parallel to an area. Mass or weight of the test port based on the category that you want to achieve. Shear stress normal stress is a result of load applied perpendicular to a member. In a previous lesson we have learned about how a bending moment causes a normal stress this normal stress often dominates the design criteria for beam strength but as beams become short and thick a transverse shear stress.

Shear loading on plate. See barrett for more details on estimates of bearing allowables. Shear stress ave n mm 2 lbs in 2 f applied force n lbs π pi or 3 14157 r radius mm in d diameter mm in bearing stress equation. Like in bending stress shear stress will vary across the cross sectional area.

Almost any length width thickness or material. Looking again at figure one it can be seen that both bending and shear stresses will develop. Easier and more accurate alignment than two or more butt hinges. Many load bearing points equal to the number of knuckles per leaf.